Production Function in the Short Run

The short run production production assumes there is at least one fixed factor input

Production Functions

• The production function relates the quantity of factor inputs used by a business to the amount of output that result.

We use three measures of production and productivity:

Total product (total output). In manufacturing industries such as motor vehicles, it is straightforward to measure how much output is being produced. In service or knowledge industries, where output is less “tangible" it is harder to measure productivity.

Average product measures output per-worker-employed or output-per-unit of capital.

Marginal product is the change in output from increasing the number of workers used by one person, or by adding one more machine to the production process in the short run.

The length of time required for the long run varies from sector to sector. In the nuclear power industry for example, it can take many years to commission new nuclear power plant and capacity. This is something the UK government has to consider as it reviews our future sources of energy.

Short Run Production Function

• The short run is a time period where at least one factor of production is in fixed supply
• A business has chosen its scale of production and sticks with this in the short run
• We assume that the quantity of plant and machinery is fixed and that production can be altered by changing variable inputs such as labour, raw materials and energy

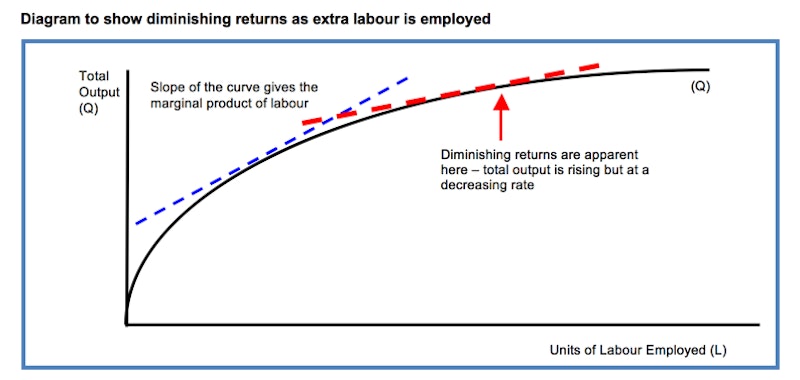
Diminishing Returns

• In the short run, the law of diminishing returns states that as more units of a variable input are added to fixed amounts of land and capital, the change in total output will first rise and then fall
• Diminishing returns to labour occurs when marginal product of labour starts to fall. This means that total output will be increasing at a decreasing rate

What might cause marginal product to fall?

One explanation is that, beyond a certain point, new workers will not have as much capital equipment to work with so it becomes diluted among a larger workforce I.e., there is less capital per worker.

In the following numerical example, we assume that there is a fixed supply of capital (capital = 20 units) to which extra units of labour are added to the production process.

• Initially, marginal product is rising – e.g. the 4^th worker adds 26 to output and the 5^th worker adds 28 and the 6^th worker increases output by 29.
• Marginal product then starts to fall. The 7^th worker supplies 26 units and the 8^th worker just 20 added units. At this point production demonstrates diminishing returns.
• Total output will continue to rise as long as marginal product is positive
• Average product will rise if marginal product > average product

Criticisms of the Law of Diminishing Returns

• How realistic is this assumption of diminishing returns? Surely ambitious and successful businesses will do their level best to avoid such a problem emerging?

• It is now widely recognised that the effects of globalisation and the ability of trans-national businesses to source their inputs from more than one country and engage in transfers of business technology, makes diminishing returns less relevant

• Many businesses are multi-plant meaning that they operate factories in different locations – they can switch output to meet changing demand